UNIFOR 2022-1 - Questão 03

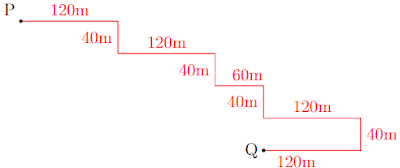
Ana, Bia e Pedro amam correr. Durante o período de isolamento social rígido, correram separados dentro do condomínio onde moram, seguindo os trajetos mostrados na figura abaixo.


O percurso feito por Ana consistia em ir do ponto P ao ponto S e de lá para P, seguindo o mesmo trajeto, duas vezes. O percurso feito por Bia consistia em ir do ponto P ao ponto Q e de lá retornar para Q, pelo mesmo trajeto, quatro vezes. Já o percurso feito por Pedro consistia em ir do ponto P ao ponto R e de lá retornar para P, pelo mesmo trajeto, três vezes. Em um determinado dia Ana, Bia e Pedro fizeram os seus respectivos percursos com velocidade constante de 1,6 m/s, 2 m/s e 2,1 m/s, respectivamente. Sendo $T_A$, $T_B$ e $T_P$ o tempo gasto por Ana, Bia e Pedro, respectivamente, para completar seu treino nesse dia, é correto afirmar que

(Use √13 = 3,6)

  1. $T_A < T_B < T_P$.
  2. $T_P < T_B < T_A$.
  3. $T_B < T_A < T_P$.
  4. $T_A < T_P < T_B$.
  5. $T_B = T_P < T_A$.


Solução

Para descobrir a resposta da questão basta saber o tempo gasto de Pedro e Bia.
Vamos calcular o trajeto de Pedro primeiro.



Somando todos os valores vamos ter o valor apenas de uma ida, que é 980m. Como o valor do trajeto é de ida e volta vamos multiplicar esse valor por 2, então o valor do trajeto fica 1960m. Agora vamos calcular o total de metros que ele percorreu, como no caso ele percorreu esse trajeto 3 vezes vamos multiplicar o valor do trajeto de Pedro por 3, que então fica 5880m. E por fim vamos calcular o tempo que durou pra fazer a caminhada, sabemos que Pedro possui uma velocidade constante de 2,1 m/s, então basta dividir o total de metros que ele percorreu pela sua velocidade, e então o resultado disso dá em 2800 segundos. Vamos fazer os mesmos cálculos com o trajeto de Bia.



Valor da ida(Bia): 700m

Valor do trajeto(Bia): 1400m

Total de metros percorrido(Bia): 5600m

Tempo da caminhada(Bia): 2800 s

Percebemos que o tempo de caminhada de Bia e de Pedro são iguais, e o único item onde o tempo de Bia e de Pedro são iguais é no item E.

Item correto: E

Questão 02          Questão 04

Assinar: Postagens (Atom)